Deze site maakt gebruik van cookies, zodat wij je de best mogelijke gebruikerservaring kunnen bieden. Cookie-informatie wordt opgeslagen in je browser en voert functies uit zoals het herkennen wanneer je terugkeert naar onze site en helpt ons team om te begrijpen welke delen van de site je het meest interessant en nuttig vindt.
Mediaan
Wat is de Mediaan?
De mediaan is een maat van locatie die we gebruiken in de beschrijvende statistiek. Het is het middelpunt in een set gesorteerde getallen. Hiermee bedoelen we: de mediaan verdeelt de dataset in twee gelijke delen: 50 procent van alle datapunten bevinden zich aan de ene kant van de mediaan en 50 procent aan de andere kant.
Naast de mediaan, zijn er nog een aantal andere maten van locatie in een dataset aan te wijzen.
- Het gemiddelde, je kent ‘m vast wel: de som van alle datapunten in een dataset gedeeld door het aantal datapunten.
- De modus, iets minder bekend: de meest voorkomende waarde in een set getallen.
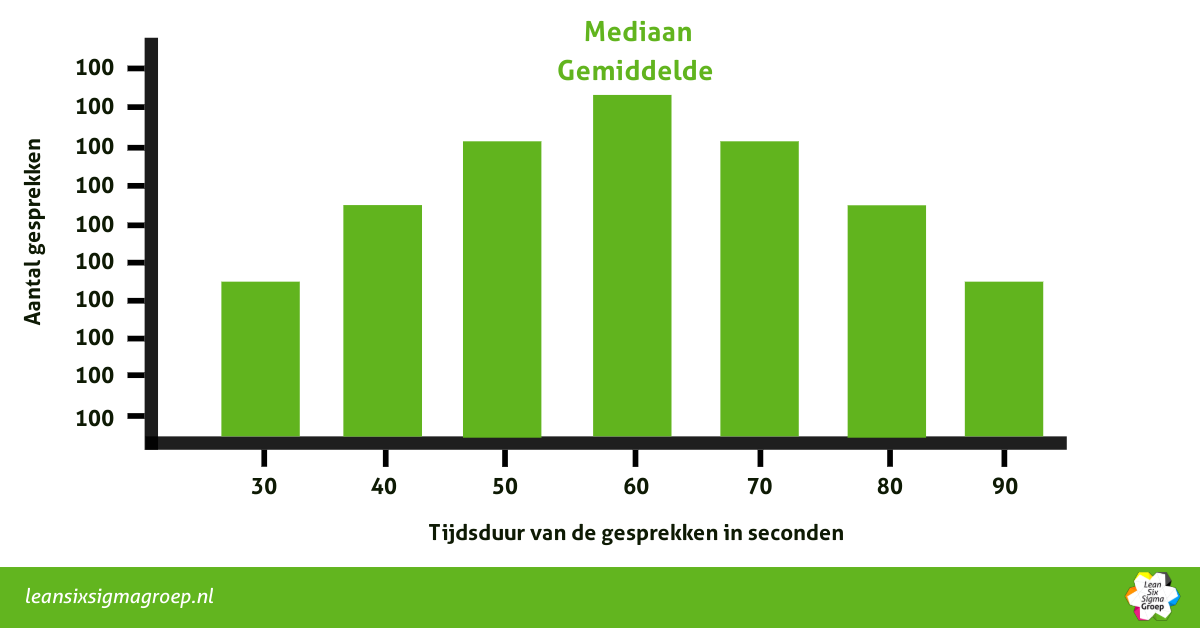
Stel, een callcenter heeft van duizend klantgesprekken de lengte van elk telefoontje bijgehouden. Als ze elk datapunt een plekje geven op een horizontale as (links staan hele korte telefoontjes en de langste telefoontjes staan helemaal rechts), dan kunnen we letterlijk de locaties gaan aanwijzen: hier bevindt het gemiddelde, hier de modus en hier de mediaan.
De locatie wordt vaak weergegeven door de mediaan of het gemiddelde, afhankelijk van de data waar we naar kijken. Het geeft aan waar de gegevens zich concentreren en het helpt bij het begrijpen van de verzameling van gegevens. Het is een soort samenvatting van het gehele verhaal.
Zo kunnen we zeggen dat het gemiddelde telefoontje 1 minuut duurt, of dat de mediaan van deze datapunten ligt op 55 seconden.
Waarom de mediaan belangrijker dan het gemiddelde?
Hoewel het gemiddelde een nuttige maatstaf is, kan deze worden beïnvloed door uitschieters (extreme waarden) waardoor het géén goede weergave meer is van de werkelijkheid. De mediaan is robuuster tegen uitschieters en geeft een betere indicatie van het centrale punt in de data, vooral wanneer de dataset niet normaal verdeeld is.
Stel, je wilt weten wat een Freelance Scrum Master zoal verdient.
Je vraagt het uurtarief van vijf Scrum Masters in je LinkedIn-netwerk op en zet deze gesorteerd op een rij:
- Het gemiddelde uurtarief is €72
- Het mediaan uurtarief is €70
Deze twee komen nu nog aardig overeen.
Maar wat nou als je een paar dagen later in contact komt met een getrouwd stel. Zowel hij als zij werken allebei als Scrum Master, hebben heel wat ervaring en werken voor een veelbelovende Start up in New York waar de tarieven nèt even wat hoger liggen. Deze scrum masters verdienen beide maar liefst €300 per uur.
De reeks wordt dan als volgt:
Het gemiddelde schiet dan omhoog naar ± €137
De mediaan? Die komt op €80 te staan.
Door deze uitschieters geeft het gemiddelde je een behoorlijk vertekend beeld van wat een gemiddelde Scrum Master verdient.
De mediaan representeert nu eigenlijk veel beter het uurtarief van de meeste Scrum Masters in de dataset.
Hoe selecteer je de mediaan als je een even aantal getallen hebt?
Als je een even aantal datapunten hebt, dan zit er géén getal exact in het midden. Je berekent dan het gemiddelde van de twee middelste datapunten. Hieronder een voorbeeld:
Je reeks getallen is als volgt:
De twee middelste getallen zijn €70 en €80.
- Gemiddeld is dat €75
- De mediaan wordt dan: €75
Wat is een normale verdeling?
Een belangrijke regel in de wondere wereld van statistiek is dat wanneer de data normaal verdeeld is, het gemiddelde een goede maatstaf is, maar wanneer de data niet normaal verdeeld is, je vaak meer hebt aan de mediaan omdat deze minder gevoelig is voor uitschieters.
Normaal verdeelde data, ook bekend als een klokvormige verdeling, heeft specifieke kenmerken. In normaal verdeelde data zijn het gemiddelde, de mediaan en de modus allemaal op hetzelfde punt te vinden. Namelijk: in het midden.
In 1794 is dit fenomeen door sterrenkundige Carl Friederich Gauss ontdekt en in het begin van de 19e eeuw door Adolphe Quetelet losgelaten op mens en dieren. En wat blijkt? Heel veel variabelen zijn normaal verdeeld!
Denk aan: de lengte van een groep personen, de schoenmaat, het BMI, de borstomtrek van kangoeroes, het aantal stekels op een egel; en ga zo nog maar even door. Het fenomeen komt dus vaak voor en wordt zodoende als normaal beschouwd.
Hoe kun je zien of data wel of niet normaal verdeeld is?
Je kunt de verdeling van data vooral goed zien door het in een histogram te zetten.
De datapunten zijn verdeeld in een symmetrisch patroon rond het centrale punt, met de meeste waarden dicht bij het gemiddelde en geleidelijk afnemend in frequentie naarmate ze verder van het gemiddelde af staan.
Ook kun je je dataset inladen in statistische programma’s zoals Minitab of SPSS. Het programma laat je dan weten of jouw dataset wel of niet normaal verdeeld is.