Boxplot

Wat is een boxplot?

De boxplot is ontwikkeld in 1962 door de Amerikaanse geleerde John Tukey. Een boxplot (In het Nederlands ook wel een ‘snorrendoos’ genoemd) biedt een visuele weergave van continue data, waarmee enkele cruciale kenmerken van de dataset in één oogopslag duidelijk worden. Het is een effectieve grafische tool om de verschillen tussen diverse dwarsdoorsneden van data helder te presenteren.

Neem bijvoorbeeld de doorlooptijd van een specifieke processtap; als je de variatie tussen verschillende individuen binnen die stap wilt begrijpen, is de doorlooptijd een voorbeeld van continue data. Na het meten van minimaal 30 doorlooptijden kun je niet alleen het gemiddelde bepalen, maar ook de mediaan (de middelste waarde in de gerangschikte data) en ook de spreiding vaststellen: wat was de snelste doorlooptijd en wat was de langste doorlooptijd per persoon.

Hoewel het mogelijk is om gemiddelden, medianen en spreiding met behulp van MS-Excel naast elkaar te plaatsen in een tabel, kan deze presentatie vaak als abstract en moeilijk leesbaar worden ervaren. Echter, maak je er een grafische weergave van met een boxplot, dan kun je in één oogopslag de variatie in doorlooptijden van de verschillende afdelingen of individuen met elkaar vergelijken.

Hoe lees je een boxplot af?

Hieronder zie je een boxplot. Wat je ziet is dat de gegevens in een grafiek worden weergegeven op de volgende manier: de data wordt van laag naar hoog gerangschikt. Vervolgens staat de middelste 50% van de gegevens in het midden, in de ‘box’. Daaromheen zie je de rest van de gegevens met een streepje weergegeven, dus de eerste 25% eerst, dan de box, en dan de laatste 25%. Wat je ook ziet is de mediaan, dat is de middelste waarde. De streepjes, of whiskers of snorharen kunnen een maximale lengte hebben van 1,5 keer de box. Als er data is buiten deze lengte, dan worden het sterretjes, en zijn het outliers. Als je data hebt van meerdere groepen kun je meerdere boxplots naast elkaar krijgen, en zie je dus gelijk de verschillen tussen de groepen.

Hoe kun je de boxplot toepassen?

Allereerst als manier om naar je data te kijken, als bijvoorbeeld de tijd waarin mensen de 1000 meter rennen. Dat kan in 1 box. Maar je kunt ook meerdere groepen naast elkaar leggen. Zo zou je kunnen vaststellen dat de ene groep gemiddeld het snelst is, maar ook ontzettend veel varieert in doorlooptijd ten opzichte van de andere groep. Die andere groep is gemiddeld gezien dan wel wat trager, maar is wel betrouwbaarder: de snelste tijd en traagste tijd liggen een stuk dichter bij de gemiddelde doorlooptijd. Je weet dus in ieder geval wel beter waar je bij die groep aan toe bent.

Het vaststellen van de verschillen tussen groepen is stap één, stap twee is onderzoek uitvoeren: wáárom zijn deze verschillen ontstaan? Ook kun je outliers identificeren: datapunten die significant afwijken van de rest van de data. Om in het voorbeeld van hierboven te blijven: dit zouden de enorm snelle of ongelooflijk tage doorlooptijden zijn. Ze passen eigenlijk niet binnen wat je zou verwachten als je de andere datapunten ziet. Deze outliers worden visueel gemaakt als puntjes buiten de snorrendoos.

Ook hier geldt dat we aan de hand van deze conclusie een nader onderzoek kunnen starten: wat is er precies gebeurt waardoor deze outliers zijn gemeten?

Een andere toepassing is het inzichtelijk maken van trends. Zo zou je de doorlooptijden van een bepaald proces in kaart kunnen brengen voor de maand januari. Doe je dit ook voor februari en maart, dan kun je aan de hand van de drie boxplots naast elkaar al snel concluderen of het proces verbeterd is op gebied van:

Doorlooptijd: staan de gemiddelden en medianen van de boxplot van februari lager dan die van januari? En die van maart ook weer lager ten opzichte van februari?
Betrouwbaarheid: zien we dat de boxplots per maand korter worden, dan kunnen we concluderen dat de doorlooptijden minder van elkaar variëren en het proces dus steeds wat betrouwbaarder wordt.

Waar kun je een boxplot zoal voor gebruiken?

Om de kracht van de boxplot wat beeldender te maken, volgen hier een aantal ideeën ter toepassing:

Analyse van klanttevredenheid:

Boxplots kunnen worden gebruikt om de tevredenheid van klanten met verschillende producten of diensten te vergelijken.
Bedrijven kunnen boxplots gebruiken om de tevredenheid van klanten met de klantenservice te vergelijken over verschillende kanalen, zoals telefoon, e-mail of chat.

Vergelijken van online winkelprestaties:

Webwinkelbedrijven kunnen boxplots gebruiken om de gemiddelde bestelgrootte, de levertijden en de retourpercentages te vergelijken tussen verschillende platforms of marketingcampagnes.
Boxplots kunnen worden gebruikt om de prestaties van verschillende productcategorieën of prijsklassen te analyseren.

Onderzoek naar sportprestaties:

Sportteams kunnen boxplots gebruiken om de prestaties van atleten te vergelijken op basis van verschillende factoren, zoals leeftijd, gewicht, trainingservaring of competitieniveau.
Boxplots kunnen worden gebruikt om de prestaties van teams te analyseren over verschillende wedstrijden of seizoenen.

Analyse van medische gegevens:

Onderzoekers kunnen boxplots gebruiken om de bloeddruk, cholesterolniveaus of lichaamsmassa-index (BMI) te vergelijken van verschillende patiëntengroepen.
Boxplots kunnen worden gebruikt om de effectiviteit van verschillende medicijnen of behandelingen te evalueren.

Milieumonitoring:

Milieubewakers kunnen boxplots gebruiken om de concentraties van vervuilende stoffen in de lucht of het water te vergelijken tussen verschillende locaties of tijdstippen.
Boxplots kunnen worden gebruikt om de effecten van milieubeleid of -initiatieven te analyseren.

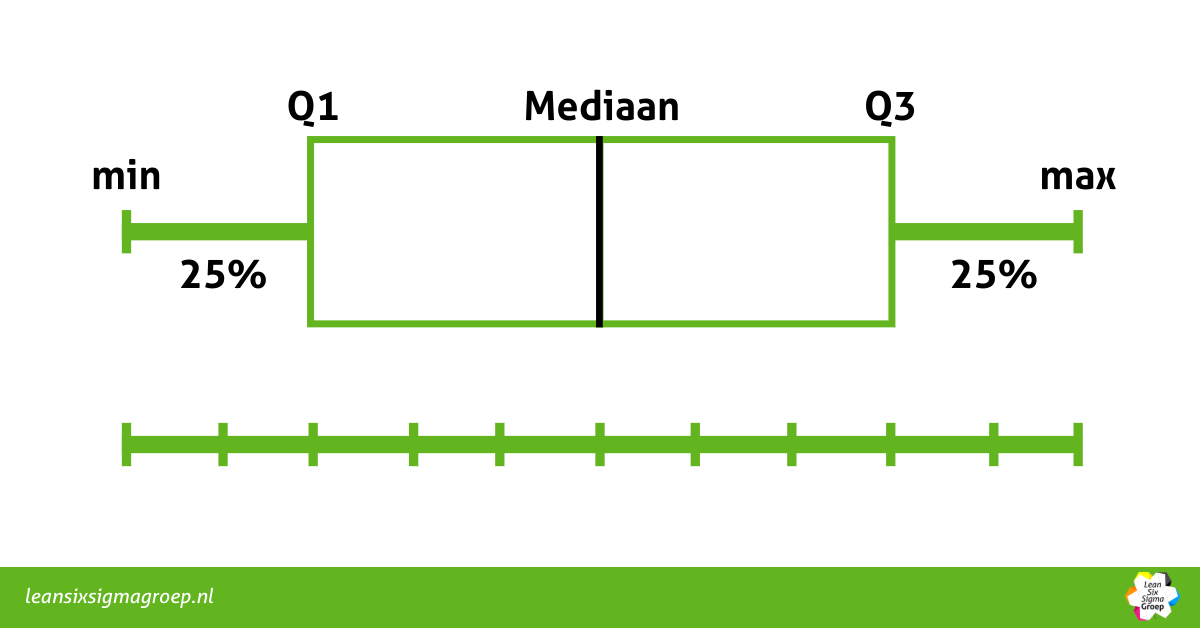
Hoe wordt de boxplot gemaakt?

In eerste instantie wordt de data geordend door alle waarnemingen van laag naar hoog te rangschikken. Vervolgens wordt de dataset opgedeeld in vier gelijke delen, ook wel kwartielen genoemd. Deze kwartielen hebben specifieke grenswaarden, zoals bijvoorbeeld Q1 in het onderstaande voorbeeld. Q1 geeft aan welke waarde de begrenzing vormt van de eerste 25% van de geordende waarnemingen. Q2 komt overeen met de mediaan, oftewel de grens van de eerste 50% van de geordende waarnemingen. Q3 vertegenwoordigt de grens van 75%.

Het interessante aspect hierbij is dat het verschil in waarde tussen Q3 en Q1 de spreiding aangeeft van de middelste 50% van de waarnemingen, bekend als de interkwartielrange. Waarnemingen onder Q1 en boven Q3 worden weergegeven door de ‘snorharen’ van de boxplot. De lengte van deze snorharen is altijd maximaal 1.5 keer de interkwartielrange. Observaties die zich verder uitstrekken dan deze maximale lengte worden beschouwd als de hierboven besproken outliers en vormen altijd aanleiding voor nader onderzoek.

Onderstaande afbeelding laat het aantal fouten per maand zien van 4 verschillende afdelingen (A, B, C en D);