Wat is Anova?
ANOVA is een begrip in de statistiek en staat voor variantenanalyse, in het Engels ANalysis Of VAriance. Het is een hypothesetoets om na te gaan of de gemiddelden van drie of meer groepen significant van elkaar verschillen of dat de verschillen op toeval berusten.
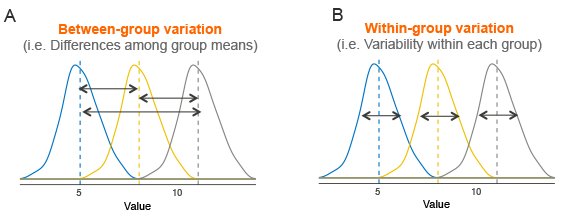
De toets meet het verschil in twee delen; de variantie bínnen de groepen en de variantie tússen de groepen wordt met elkaar vergeleken. Als een van de groepen significant verschilt in gemiddelde waarde, resulteert dat in een lage P-waarde voor de gehele test. Als P > 0,05, dan is er geen verschil tussen de gemiddelden van de groepen. Bij P < 0,05 dan is er wel een verschil tussen de gemiddelden van de verschillende groepen.
De analysetechniek is bedacht door de Britse statisticus en geneticus Ronald Aylmer Fisher in de jaren 1920 – 1930.
ANOVA en SIX SIGMA
Binnen Six Sigma draait het om het terugbrengen van variatie, van spreiding. Dan is de analyse van de variatie dus van essentieel belang. Met de ANOVA-toets kunnen we aantonen of er verschil in variantie zit tussen de gemiddelden van meer dan drie groepen data.
Voorbeeld, om de ANOVA-toets te verduidelijken
We vergelijken de lichaamslengte van verschillende sporters, bv. volleyballers, voetballers en wielrenners. Is de lengte in deze groepen gemiddeld genomen dezelfde, of zijn er systematische verschillen? Het is logisch om te denken dat binnen elke groep verschillen in lengte zijn. Niet alle wielrenners zijn even lang en ook niet alle voetballers en volleyballers. De vraag is of er ook tussen de groepen verschillen zijn. Is de gemiddelde lengte van voetballers anders dan de gemiddelde lengte van wielrenners? De gemiddelden van de drie groepen zullen niet precies aan elkaar gelijk zijn. We vragen ons daarom af of de verschillen tússen de groepen vergelijkbaar zijn met of veel groter zijn dan de verschillen bínnen de groepen. Daartoe worden steekproeven genomen en de totale variantie, die een maat is voor de variatie, wordt geanalyseerd in twee componenten; de variantie binnen de groepen en de variantie tussen de groepen. Door het vergelijken van deze twee componenten kan beslist worden of de groepsgemiddelden als verschillend beschouwd mogen worden of niet.
Het bovenstaande is een voorbeeld van een eenweg-variantieanalyse (one-way-anova). Er is sprake van één factor (lengte) en drie groepen (volleyballers, voetballers en wielrenners). Bij een tweeweg-variantenanalyse (two-way-anova) wordt naast de lengte bv. ook gekeken of het geslacht (man-vrouw) van invloed is op het mogelijk verschil tussen de groepen.
Hulpmiddel bij ANOVA
Het uitvoeren van de ANOVA kan handmatig gebeuren maar dat is een ingewikkelde en tijdrovende rekenopgave. Er zijn allerlei statistiekprogramma’s op de markt waar de data eenvoudig ingevoerd kan worden en waarbij de uitkomst binnen enkele seconden zichtbaar op het scherm wordt weergegeven. Zo kan gebruik gemaakt worden van Minitab of SPSS, maar ook met behulp van MS Excel kan een ANOVA worden uitgevoerd.