De Normale Verdeling

De Normale Verdeling: Wat is het?

De Normale Verdeling, ook wel de Gausscurve of Bell curve genoemd, is een symmetrische kansverdeling die vaak voorkomt in de natuurlijke wereld. Het wordt gekenmerkt door een centrale piek en afnemende waarschijnlijkheid aan beide zijden. De verdeling wordt volledig bepaald door twee parameters: het gemiddelde (μ) en de standaardafwijking (σ).

• μ (mu): Het gemiddelde, dat het centrum van de curve vertegenwoortigt. Het gemiddelde geeft aan wat de typische waarde in een dataset is.
• σ (sigma): De standaardafwijking, die de breedte van de curve aangeeft. De standaardafwijking vertelt ons hoe ver data verspreid is ten opzichte van het gemiddelde.

Het gemiddelde geeft het centrale punt van de verdeling aan, terwijl de standaardafwijking de mate van spreiding rond het gemiddelde aangeeft. De standaardafwijking, ofwel de spreiding is de gemiddelde afstand tot het gemiddeld.

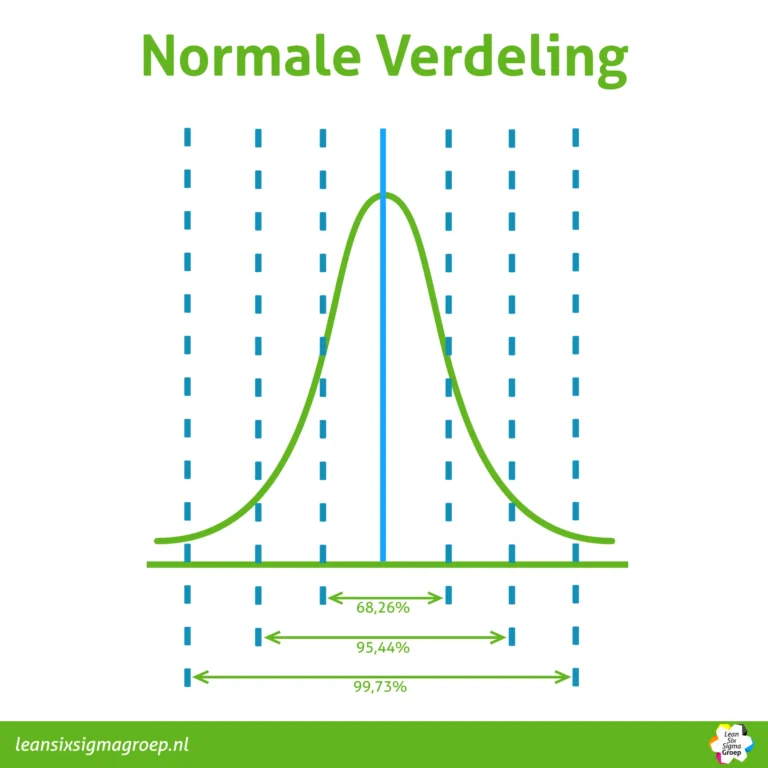
Een belangrijke eigenschap van de normale verdeling is de empirische regel (ook bekend als de 68-95-99.7 regel). Ongeveer 68% van de gegevens ligt binnen één standaardafwijking van het gemiddelde, ongeveer 95% ligt binnen twee standaardafwijkingen, en bijna 99,7% ligt binnen drie standaardafwijkingen. In de praktijk betekent dit dat de voorspelbaarheid van de uitkomsten toeneemt. Immers als je weet dat de normale verdeling van toepassing is op de uitkomsten van een proces, kun je met een relatief kleine steekproef al vaststellen hoe het proces momenteel presteert. En dat is heel handig om voorspellingen te doen in de toekomst.

 

Datawetenschap

In de datawetenschap helpt de normale verdeling wetenschappers om:

• Trends te identificeren in grote datasets. Door te kijken naar de vorm van de curve, kunnen wetenschappers zien of de data zich symmetrisch rond het gemiddelde verdeelt of juist scheef is verdeeld.
• Uitschieters te detecteren. Data kan afwijkingen bevatten die significant afwijken van de rest. De normale verdeling helpt wetenschappers om deze outliers te identificeren, die mogelijk duiden op meetfouten of ongewone gebeurtenissen.
• De waarschijnlijkheid van toekomstige gebeurtenissen te voorspellen. Door te begrijpen hoe data zich rond het gemiddelde verspreidt, kunnen wetenschappers statistische modellen bouwen om de waarschijnlijkheid van toekomstige uitkomsten te voorspellen.

Kwaliteitscontrole

In de kwaliteitscontrole, met name in Six Sigma, is de normale verdeling een onmisbaar hulpmiddel voor:

• Het analyseren van processen en het identificeren van knelpunten. Door de werkelijke procesdata te vergelijken met de verwachte verdeling (gebaseerd op de gemiddelde waarde en standaardafwijking), kunnen bedrijven identificeren waar hun processen afwijken van de specificaties.
• Het meten van de proceskwaliteit met behulp van defecten per miljoen mogelijkheden (DPMO). DPMO is een metric gebaseerd op de normale verdeling waarmee de hoeveelheid defecten in een proces kan worden gekwantificeerd.
• Het optimaliseren van processen door gerichte verbeteringen door te voeren. Door de oorzaken van procesvariabiliteit te achterhalen met behulp van de normale verdeling, kunnen bedrijven data gebruiken om gerichte verbeteringen door te voeren en de proceskwaliteit te verhogen.

Een belangrijke eigenschap van de Normale Verdeling is de empirische regel (ook bekend als de 68-95-99.7 regel). Deze regel stelt dat:

• 68%van de data binnen één standaardafwijking van het gemiddelde valt. Dit betekent dat in een dataset met 100 datapunten, we 68 datapunten verwachten binnen 1 standaardafwijking van het gemiddelde.
• 95% van de data binnen twee standaardafwijkingen van het gemiddelde valt. In dezelfde dataset verwachten we 95 datapunten binnen 2 standaardafwijkingen van het gemiddelde.
• 99,7%van de data binnen drie standaardafwijkingen van het gemiddelde valt. Dit betekent dat we in de meeste datasets 99,7% van de datapunten binnen 3 standaardafwijkingen van het gemiddelde verwachten.

De normale verdeling is een krachtig instrument voor het begrijpen en analyseren van data. Door de positie van datapunten te bekijken ten opzichte van het gemiddelde en de standaarddeviatie, kunnen we de dataverspreiding interpreteren. Dit helpt ons bij het voorspellen van uitkomsten, aangezien we kunnen inschatten hoeveel data we binnen een bepaalde range van het gemiddelde verwachten. Bovendien wijst data die buiten de normale verdelingscurve valt mogelijk op afwijkingen of fouten, waardoor we deze nader kunnen onderzoeken. Deze regel is dus van onschatbare waarde voor het interpreteren van dataverspreiding, het voorspellen van uitkomsten en het bepalen van de waarschijnlijkheid van afwijkingen.

Hoe ontstaat de Normale Verdeling?

De Normale Verdeling ontstaat vaak als het resultaat van een groot aantal onafhankelijke, willekeurige invloeden op een bepaalde meting. In de natuur komt de normaal verdeling vaak voor. Als je bijvoorbeeld kijkt naar de lengte van de blaadjes aan een eikenboom dan zullen deze blaadjes een gemiddelde hebben, en het ene blaadje is wat langer of korter dan het andere blaadje. Als je alle blaadjes opmeet dan kun je uit de 1000 blaadjes van een boom het gemiddelde uitrekenen en de spreiding. Stel je voor dat het gemiddelde van de blaadjes 9 cm is en de spreiding 1 cm. Dan weet je dus dat 68% van de blaadjes tussen de 8 en de 10 cm zijn. En 99,7% tussen de 6 en de 12 cm. De normaal verdeling is vaak van toepassing op een toevalsproces. Als er een speciale oorzaak is die blaadjes langer maakt (wat bij blaadjes niet vaak het geval is maar bijvoorbeeld wel met doorlooptijden) dan is de normaal verdeling niet meer van toepassing.

Uiteindelijk gaat alles naar de normaal verdeling toe. Dit wordt ook wel de “centrale limiettheorie” genoemd. Het centrale limiettheorema stelt dat als we herhaaldelijk steekproeven uit een willekeurige populatie nemen en het gemiddelde van elke steekproef berekenen, deze gemiddelden een Normale Verdeling zullen volgen, zelfs als de oorspronkelijke populatie geen normale verdeling heeft. Dit maakt de Normale Verdeling een krachtig hulpmiddel bij het modelleren en begrijpen van verschillende situaties, van het meten van lengtes en gewichten tot het voorspellen van klantgedrag in bedrijven. Het helpt dus ook bij het inschatten van toekomstige data.

Toepassing van de Normale Verdeling in Six Sigma

Six Sigma is een methodologie die gericht is op het verbeteren van de kwaliteit van processen door spreiding te verminderen en defecten te minimaliseren. Deze methodologie maakt gebruik van de Normale Verdeling om gegevensanalyse te ondersteunen. Zoals gezegd gebruiken we de verdeling vaak om een model te maken van hoe een proces zich zal gedragen. Je kunt dit model maken als je uit historische gegevens kunt halen dat een proces normaal verdeeld is. Hiervoor heb je dus wel een meting nodig, maar vaak volstaan hier al 30 datapunten voor. En als je weet dat een proces normaal verdeeld is dan kan je verder gaan rekenen bijvoorbeeld in de volgende onderdelen:

1. Standaardafwijking en Z-score:

In het Six Sigma-proces wordt de standaardafwijking als een belangrijke maatstaf gebruikt om de variabiliteit of spreiding van een proces te beoordelen. Met behulp van de Z-score wordt de klantwens gekoppeld aan het proces. Hiermee kun je meten hoeveel standaardafwijkingen de klantwens zich van het gemiddelde bevindt. Dit helpt bij het bepalen van hoe goed een proces is ten opzichte van de klantwens. De Z-score geeft aan hoe veel keer een standaardafwijking past binnen het gebied tussen het gemiddelde en een grenswaarde van de klantwens. Het aantal dat erbuiten valt correspondeert vervolgens met een kans op fouten, de zogenaamde Probility of Defect. Hiermee kun je dan eenvoudig aangeven hoe groot de kans op overschrijding van de klantwens is en de procesprestatie aangeven. De Z-waarde noemen we ook wel Sigma level, waarmee de koppeling met Six Sigma kan worden gelegd. Hier komt dus de naam 6 sigma vandaan. Six sigma koppelt dus klantwens aan proces.

2. Defecten per miljoen mogelijkheden (DPMO):

Met de normale verdeling en Z-scores kan Six Sigma de DPMO berekenen, wat het aantal defecten per miljoen mogelijkheden aangeeft. Dit helpt bij het kwantificeren van de prestaties van een proces en het stellen van realistische doelen voor verbetering.

3. Control charts:

Dit is een grafiek waarmee je de uitkomsten van je proces in de tijd laat zien met daarin het gemiddelde en 3 keer de standaarddeviatie. Hiermee kun je zien of je proces onder controle is of dat er wat anders aan de hand is. Met behulp van de bekende standaardafwijking kun je zo sneller, eenvoudiger én met minder kosten uit de metingen herleiden of de uitkomsten binnen een bepaalde bandbreedte blijven. Deze bandbreedte wordt, bij normaal verdeelde data, berekend door vanaf het gemiddelde 3 keer de standaardafwijking op te tellen én af te trekken: dit betekent dus dat normaal gesproken 99,7% van de gegevens tussen deze bandbreedte blijft. Daardoor ontstaat een Upper Control Limit (UCL) én een Lower Control Limit (LCL). De ruimte tussen beide waarden is dan het gebied waarvan je mag verwachten dat de uitkomsten zich zullen bewegen. Hoe kleiner de standaardafwijking, hoe dichter de UCL en LCL bij elkaar zullen liggen. De datapunten die vervolgens met enige variatie binnen de UCL en LCL liggen vormen de zogenaamde “common cause variation” en geven aan hoe stabiel het proces is. Datapunten die toch buiten de bandbreedte van UCL en LCL vallen, duiden we aan met “special cause variation” en die zijn aanleiding om alert te worden. Deze uitzonderingsgevallen kun je vervolgens onderzoeken, om erachter te komen waar de afwijkingen vandaan komen. Als er veel punten buiten de UCL/LCL liggen dan is er dus wat geks aan de hand en is het proces niet meer onder controle. Wanneer de meeste punten (299 van de 300) binnen de UCL/LCL blijven dan is het proces normaal in beweging en is er geen speciale oorzaak die leidt tot meer afwijking.

4. DMAIC-methodologie:

De DMAIC-methodologie (Define, Measure, Analyze, Improve, Control) is een integraal onderdeel van Six Sigma. In de meetfase worden gegevens verzameld en geanalyseerd om de huidige prestaties van het proces te begrijpen. De Normale Verdeling wordt vaak gebruikt om de gegevens te visualiseren en te begrijpen hoe de processen zich gedragen.

Praktisch Voorbeeld: Productieproces

Stel je een productieproces voor waarbij flessen worden gevuld met een vloeistof. Het is essentieel dat elke fles exact dezelfde hoeveelheid vloeistof bevat om aan de kwaliteitsnormen te voldoen. Het Six Sigma-team kan de normale verdeling gebruiken om de variabiliteit in het vulproces te analyseren en te verminderen.

Het team verzamelt gegevens over de vloeistofvullingen en ontdekt dat de gemiddelde vulling 500 ml is, met een standaardafwijking van 5 ml. Met behulp van de normale verdeling kunnen ze de kans berekenen dat een willekeurige fles meer of minder dan 500 ml bevat. Ze kunnen ook de DPMO berekenen om het huidige prestatieniveau te bepalen.

Door middel van DMAIC kunnen ze verbeteringen implementeren, zoals het kalibreren van de vulmachines en het trainen van het personeel. Deze aanpassingen zorgen ervoor dat het proces een veel smallere spreiding heeft (bijvoorbeeld een standaardafwijking van 1 ml), waardoor de meeste flessen zeer dicht bij de ideale 500 ml vulling liggen.

Conclusie

De Normale Verdeling speelt een cruciale rol in Six Sigma, waarbij het helpt bij het begrijpen van variabiliteit en het nemen van gegevens gestuurde beslissingen om de kwaliteit van processen te verbeteren. Het verminderen van variabiliteit en het minimaliseren van defecten leidt tot efficiëntere processen en een hogere klanttevredenheid. Six Sigma is een krachtig instrument voor organisaties die streven naar continue verbetering en het leveren van hoogwaardige producten en diensten.

Visuele toelichting Normale Verdeling

Ontgrendel de Kracht van Data met de Green Belt Opleiding

Versterk je data-analysevaardigheden en leer de kracht van de normale verdeling toe te passen in uw werk met de Green Belt Opleiding. In deze praktijkgerichte opleiding leert u:

• De concepten van de normale verdeling te begrijpen en toe te passen.
• Statistische analyses uit te voeren met behulp van de Gausscurve.
• Data te interpreteren en betrouwbare voorspellingen te doen.
• De normale verdeling te integreren in Six Sigma processen.