Wat is Correlatie?
Hoe verschilt Correlatie met Causaliteit?Correlatie is een statistische term die het verband tussen twee variabelen weergeeft. Het begrip wordt veel gebruikt in uiteenlopende wetenschappelijke disciplines, en daarbij ook binnen Lean Six Sigma. In dit artikel verkennen we wat correlatie precies inhoudt, hoe het wordt gemeten en welke valkuilen en toepassingen eraan verbonden zijn.
Wat is Correlatie?
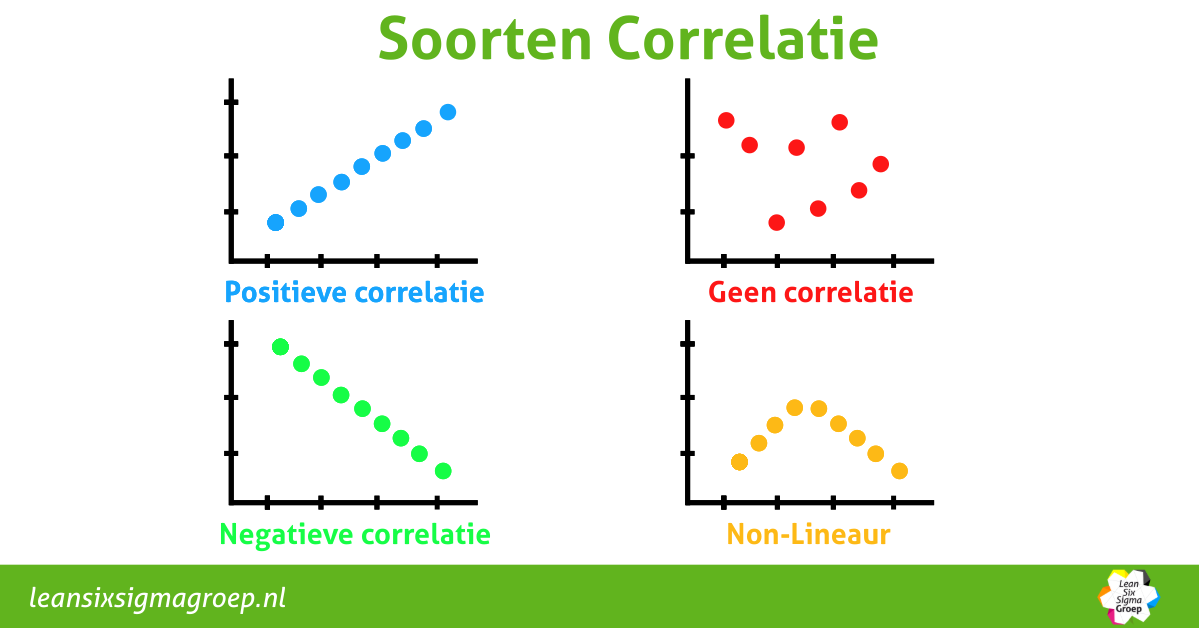
Correlatie verwijst naar de mate waarin twee variabelen samenhangen, ofwel is er een zichtbaar verband tussen de twee cijfers. Wanneer twee variabelen gecorreleerd zijn, betekent dit dat ze op een voorspelbare manier met elkaar samenhangen. Er zijn drie mogelijke “richtingen” van correlatie:
- Positieve Correlatie: Wanneer de ene variabele toeneemt, neigt de andere variabele ook toe te nemen. Bijvoorbeeld, als het aantal uren studie stijgt, stijgen de behaalde cijfers meestal ook.
- Negatieve Correlatie: Wanneer de ene variabele toeneemt, neigt de andere variabele af te nemen. Bijvoorbeeld, als de gemiddelde gereden snelheid toeneemt zal de reisduur om op bestemming te komen afnemen.
- Geen Correlatie:Er is géén voorspelbare relatie tussen de variabelen. Bijvoorbeeld, er is geen duidelijk verband tussen het aantal planten op kantoor en de hoogte van het jaarsalaris van medewerkers.
Meting van Correlatie
De meest gebruikelijke wiskundige methode om correlatie te meten is de Pearson-correlatiecoëfficiënt, vaak aangeduid met de letter R. Deze coëfficiënt kan een waarde aannemen tussen -1 en +1:
- r = +1r: Perfecte positieve correlatie
- r = −1r : Perfecte negatieve correlatie
- r = 0r: Geen correlatie
De waarde van R geeft de sterkte van de correlatie aan. Een waarde dichtbij +1 of -1 duidt op een zeer sterke correlatie, terwijl een waarde dichtbij 0 wijst op een zwakke of geen correlatie. Stel, we willen weten of er een verband is tussen het aantal uren dat iemand per week sport en de BMI (Body Mass Index). We verzamelen gegevens van 50 willekeurige personen en berekenen de correlatiecoëfficiënt tussen deze twee variabelen. We ontdekken een negatieve correlatie van -0,68. Dit betekent wiskundig dat er een redelijk sterke negatieve relatie is. In begrijpelijk Nederlands, hoe meer uren iemand sport, hoe lager zijn of haar BMI.
Voorbeeld van Correlatie in Lean Six Sigma
Stel dat een productiebedrijf een probleem heeft met variërende productkwaliteit. Het bedrijf besluit een Lean Six Sigma-project te starten om dit probleem aan te pakken. Tijdens de Measure-fase verzamelt het team gegevens over verschillende procesvariabelen, zoals temperatuur, druk, en doorvoersnelheid. Door een wiskundige correlatieanalyse uit te voeren, ontdekt het team dat er een sterke negatieve correlatie is tussen temperatuurvariatie en productkwaliteit: ofwel wanneer de temperatuur fluctueert, neemt de kwaliteit van het eindproduct af.
Met deze informatie kan het team tijdens de Analyze-fase verder onderzoeken hoe de temperatuur beter gecontroleerd kan worden. In de Improve-fase implementeert het team nieuwe temperatuurregelingssystemen en past het de procesinstellingen aan op basis van de gevonden correlaties. Uiteindelijk, in de Control-fase, blijft het team de temperatuurvariaties en productkwaliteit monitoren om ervoor te zorgen dat de verbeteringen duurzaam zijn.
Correlatie en het Verschil met Causaliteit
Eén van de meest voorkomende misvattingen over correlatie is de veronderstelling dat het automatisch causaliteit betekent. Causaliteit is de term die we gebruiken om aan te geven dat er een oorzaak – gevolg verband is. Dit is echter niet altijd het geval. Correlatie geeft slechts aan dát er een relatie bestaat tussen twee variabelen, maar het vertelt ons niets over de aard van deze relatie of de onderliggende oorzaken. Dit onderscheid is cruciaal in wetenschappelijk onderzoek en besluitvorming.
Hieronder een voorbeeld dat er een verschil is tussen correlatie en causaliteit
Stel je voor dat je een studie tegenkomt die aantoont dat er een sterke positieve correlatie bestaat tussen het aantal mensen dat een barst in zijn telefoonscherm heeft en het aantal mensen dat bovengemiddeld veel groenten eet. Het lijkt bijna alsof mensen die meer groenten eten, vaker hun telefoon laten vallen!
In werkelijkheid is er geen oorzaak – gevolg relatie tussen deze twee variabelen. Wat er mogelijk gebeurt, is dat beide statistieken beïnvloed worden door een derde factor: bijvoorbeeld, de grotere nadruk op gezondheid en welzijn kan mensen aanmoedigen om gezonder te eten en actiever te zijn, wat mogelijk ook leidt tot meer situaties waarin ze hun telefoon laten vallen, omdat ze vaker onderweg zijn of druk bezig zijn met gezonde activiteiten. Maar dat is misschien wat vergezocht.
Conclusie
Correlatie is een krachtig hulpmiddel in het bedrijfsleven en vormt een belangrijk onderdeel van Lean Six Sigma methodieken. Het helpt bedrijven om belangrijke relaties tussen procesvariabelen te identificeren, problemen te analyseren en verbeteringen te implementeren die leiden tot hogere kwaliteit en efficiëntie. Door de waarde van correlatie te begrijpen en toe te passen, kunnen bedrijven beter geïnformeerde beslissingen nemen en hun processen continu optimaliseren voor langdurig succes. Onthoud wel dat de valkuil voor het verwarren van correlatie met causaliteit op de loer ligt.