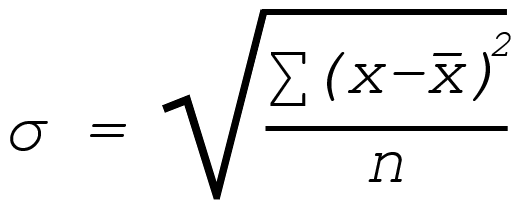Voor een steekproef wordt de noemer N vervangen door N-1.
Wanneer je de standaarddeviatie van een dataset wilt berekenen kun je hier Excel voor gebruiken. De formule voor standaarddeviatie in Excel is =STDEV.P of =STDEV.S. De P staat voor populatie en de S voor Steekproef. Of je dataset de populatie betreft of een steekproef binnen een polulatie bepaalt welke van de twee formules gebruikt wordt.
Waarom is Standaarddeviatie Belangrijk?
Standaarddeviatie geeft je inzicht in de spreiding van je data. Een lage standaarddeviatie betekent dat de data dicht bij het gemiddelde ligt, terwijl een hoge standaarddeviatie aangeeft dat de data meer verspreid is. Dit kan cruciaal zijn in verschillende contexten:
– Onderwijs: Leerkrachten kunnen zien of de prestaties van studenten variëren of redelijk consistent zijn.
– Bedrijfsleven: Bedrijven kunnen de spreiding van verkoopcijfers analyseren om betere prognoses te maken. Ook kan de standaarddeviatie helpen om te bepalen in hoeverre een proces in staat is binnen de klantspecificaties te presteren.
– Gezondheidszorg: Onderzoekers kunnen de effectiviteit van een behandeling beoordelen door te kijken naar de spreiding van resultaten.
Hoe weerhoudt de standaarddeviatie zich tot de Six Sigma methodiek?
Six Sigma is een methodologie die bedrijven gebruiken om processen te verbeteren door defecten en variabiliteit te verminderen. Het centrale idee van Six Sigma is om ervoor te zorgen dat 99.99966% van de procesuitkomsten binnen zes standaarddeviaties van het gemiddelde valt. Dit betekent dat er slechts 3,4 defecten per miljoen kansen zijn. Standaarddeviatie speelt hier een cruciale rol: door de variabiliteit in processen te meten en te minimaliseren, kunnen bedrijven de kwaliteit en efficiëntie verbeteren. Six Sigma maakt gebruik van statistische hulpmiddelen om afwijkingen in processen te identificeren en te corrigeren, en standaarddeviatie is een van de belangrijkste statistische maatstaven die hierbij wordt gebruikt.
Normaal en Niet-normaal Verdeelde Data
In veel statistische analyses wordt ervan uitgegaan dat de data normaal verdeeld is, wat betekent dat de data de vorm van een symmetrische klokcurve heeft. In een normaal verdeelde dataset vallen ongeveer 68% van de waarden binnen één standaarddeviatie van het gemiddelde, 95% binnen twee standaarddeviaties, en 99.7% binnen drie standaarddeviaties. Dit maakt het eenvoudig om voorspellingen en analyses te doen.
Echter, niet alle data volgt een normale verdeling. Bij niet-normaal verdeelde data, zoals scheve of bimodale verdelingen, kunnen de resultaten van de standaarddeviatie misleidend zijn. In dergelijke gevallen kan de standaarddeviatie niet de beste maatstaf voor spreiding zijn omdat de data asymmetrisch verdeeld is en outliers(uitschieters) de metingen sterk kunnen beïnvloeden. Voor niet-normaal verdeelde data kunnen alternatieve methoden, zoals het gebruik van de interkwartielafstand (IQR), nuttiger zijn. Deze methoden zijn minder gevoelig voor outliers en bieden een beter inzicht in de werkelijke spreiding van de data.
Een Praktisch Voorbeeld
Stel dat twee trainers, Jeroen en Laura, de scores van hun Green Belt groepen op een examen vergelijken. Beide klassen hebben een gemiddeld cijfer van 7. Echter, in de groep van Jeroen varieert het cijfer van 5 tot 9, terwijl in Laura’s groep de cijfers tussen 6,5 en 7,5 liggen. De standaarddeviatie van Jeroens klas zal hoger zijn dan die van Laura, wat aangeeft dat de scores in zijn groep meer variëren. Dit inzicht kan helpen om gerichter les te geven of aanvullende ondersteuning te bieden.
Belangrijke Aandachtspunten
– Outliers: Extreem hoge of lage waarden kunnen de standaarddeviatie sterk beïnvloeden. Het is belangrijk om te controleren op outliers en te beslissen of deze waarden moeten worden opgenomen in de analyse.
– Normale verdeling: In een normaal verdeelde dataset, valt ongeveer 68% van de waarden binnen één standaarddeviatie van het gemiddelde, 95% binnen twee en 99.7% binnen drie standaarddeviaties. Dit geeft een visueel en statistisch hulpmiddel voor het interpreteren van data.